Andrew K. Tan
PhD Candidate in Physics at MIT

Hi!
I’m currently working towards my doctorate in physics at MIT.
Feel free to reach out if you’d like to chat!
selected publications
-
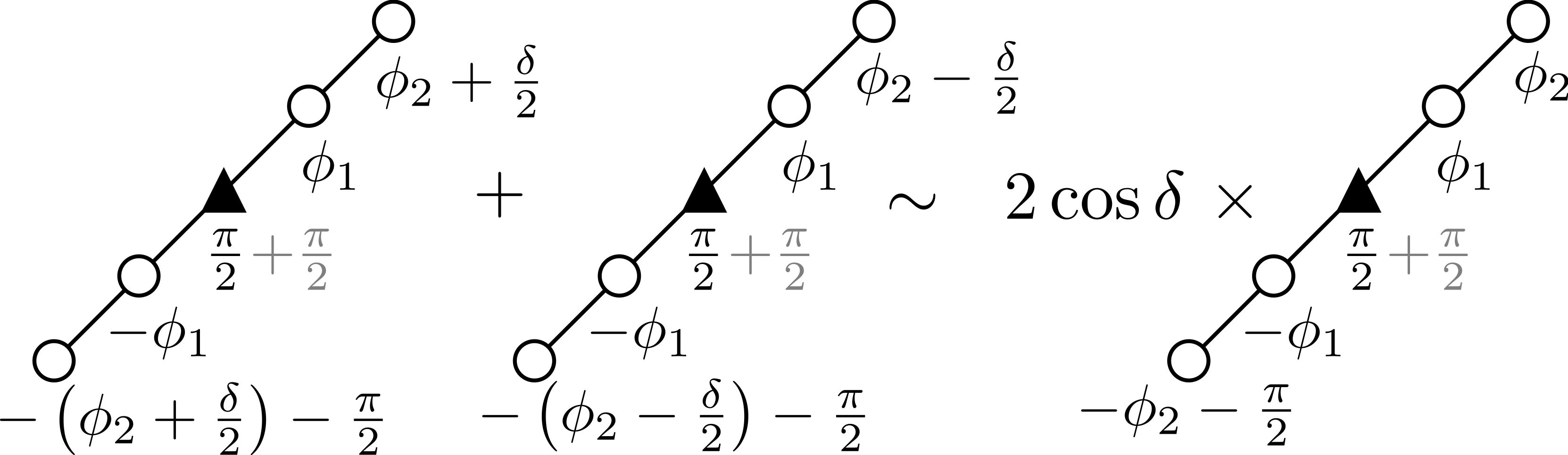 Perturbative model of noisy quantum signal processingTan, Andrew K, Liu, Yuan, Tran, Minh C, and Chuang, Isaac LPhysical Review A 2023
Perturbative model of noisy quantum signal processingTan, Andrew K, Liu, Yuan, Tran, Minh C, and Chuang, Isaac LPhysical Review A 2023Recent progress in quantum signal processing (QSP) and its generalization, quantum singular value transformation, has led to a grand unification of quantum algorithms. However, inherent experimental noise in quantum devices severely limits the length of realizable QSP sequences. We consider a model of QSP with generic perturbative noise in the signal processing basis and present a diagrammatic notation useful for analyzing such errors. To demonstrate our technique, we study a specific coherent error, that of under- or overrotation of the signal processing operator parametrized by \(ε≪1\). For this coherent error model, it is shown that while Pauli Z errors are not recoverable without additional resources, Pauli X and Y errors can be arbitrarily suppressed by coherently appending a noisy recovery QSP without the use of additional resources or ancillas. Furthermore, through a careful accounting of errors using our diagrammatic tools, we provide an upper and lower bound on the length of this recovery QSP operator. We anticipate that the perturbative technique and the diagrammatic notation proposed here will facilitate future study of generic noise in QSP and quantum algorithms.
-
 Error correction of quantum algorithms: Arbitrarily Accurate Recovery Of Noisy Quantum Signal ProcessingTan, Andrew K, Liu, Yuan, Tran, Minh C, and Chuang, Isaac LSubmitted to npj Quantum Information 2023
Error correction of quantum algorithms: Arbitrarily Accurate Recovery Of Noisy Quantum Signal ProcessingTan, Andrew K, Liu, Yuan, Tran, Minh C, and Chuang, Isaac LSubmitted to npj Quantum Information 2023The intrinsic probabilistic nature of quantum systems makes error correction or mitigation indispensable for quantum computation. While current error-correcting strategies focus on correcting errors in quantum states or quantum gates, these fine-grained error-correction methods can incur significant overhead for quantum algorithms of increasing complexity. By studying systematic errors in the modern unifying framework of quantum signal processing (QSP), we present a first step in achieving quantum error correction beyond the gate level. The technique of using device and error model specific knowledge to orchestrate the cancellation of errors at the level of the quantum subroutine can be used to augment standard quantum error correction in pursuit of fault-tolerance quantum computation.
-
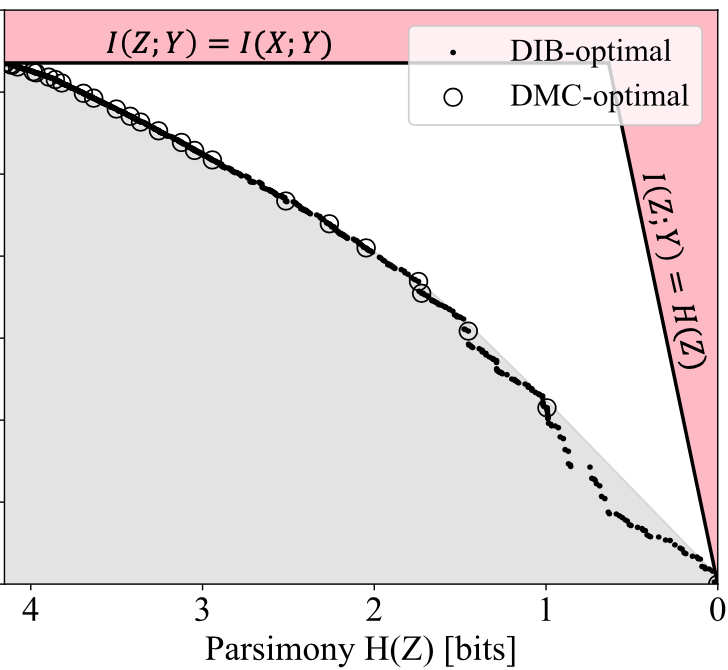 Pareto-optimal clustering with the primal deterministic information bottleneckTan, Andrew K, Tegmark, Max, and Chuang, Isaac LEntropy 2022
Pareto-optimal clustering with the primal deterministic information bottleneckTan, Andrew K, Tegmark, Max, and Chuang, Isaac LEntropy 2022At the heart of both lossy compression and clustering is a trade-off between the fidelity and size of the learned representation. Our goal is to map out and study the Pareto frontier that quantifies this trade-off. We focus on the Deterministic Information Bottleneck (DIB) formulation of lossy compression, which can be interpreted as a clustering problem. To this end, we introduce the \it primal DIB problem, which we show results in a much richer frontier than its previously studied dual counterpart. We present an algorithm for mapping out the Pareto frontier of the primal DIB trade-off that is also applicable to most other two-objective clustering problems. We study general properties of the Pareto frontier, and give both analytic and numerical evidence for logarithmic sparsity of the frontier in general. We provide evidence that our algorithm has polynomial scaling despite the super-exponential search space; and additionally propose a modification to the algorithm that can be used where sampling noise is expected to be significant. Finally, we use our algorithm to map the DIB frontier of three different tasks: compressing the English alphabet, extracting informative color classes from natural images, and compressing a group theory inspired dataset, revealing interesting features of frontier, and demonstrating how the structure of the frontier can be used for model selection with a focus on points previously hidden by the cloak of the convex hull.
-
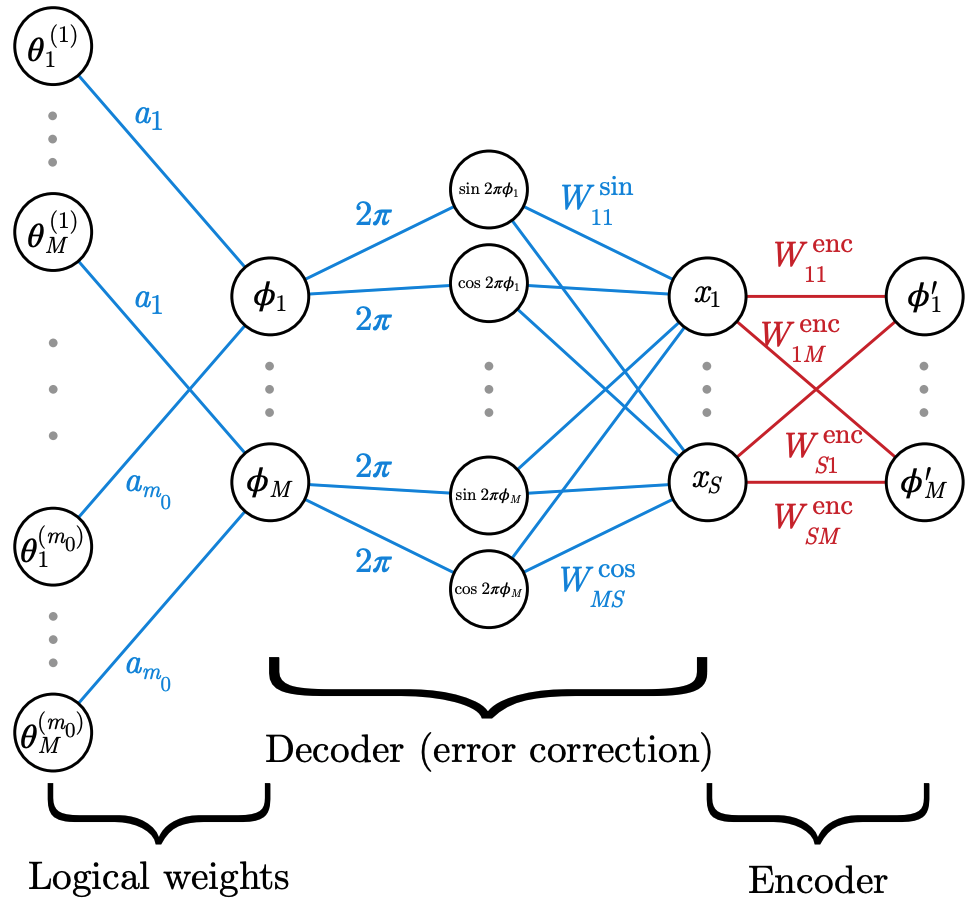 Biological error correction codes generate fault-tolerant neural networksZlokapa, Alexander, Tan, Andrew K, Martyn, John M, Tegmark, Max, and Chuang, Isaac LarXiv preprint arXiv:2202.12887 2022
Biological error correction codes generate fault-tolerant neural networksZlokapa, Alexander, Tan, Andrew K, Martyn, John M, Tegmark, Max, and Chuang, Isaac LarXiv preprint arXiv:2202.12887 2022It has been an open question in deep learning if fault-tolerant computation is possible: can arbitrarily reliable computation be achieved using only unreliable neurons? In the grid cells of the mammalian cortex, analog error correction codes have been observed to protect states against neural spiking noise, but their role in information processing is unclear. Here, we use these biological codes to show that a universal fault-tolerant neural network can be achieved if the faultiness of each neuron lies below a sharp threshold; moreover, we find that noisy biological neurons fall below this threshold. The discovery of a phase transition from faulty to fault-tolerant neural computation suggests a mechanism for reliable computation in the cortex and opens a path towards understanding noisy analog systems relevant to artificial intelligence and neuromorphic computing.
-
 Grand unification of quantum algorithmsMartyn, John M, Rossi, Zane M, Tan, Andrew K, and Chuang, Isaac LPRX Quantum 2021
Grand unification of quantum algorithmsMartyn, John M, Rossi, Zane M, Tan, Andrew K, and Chuang, Isaac LPRX Quantum 2021Quantum algorithms offer significant speedups over their classical counterparts for a variety of problems. The strongest arguments for this advantage are borne by algorithms for quantum search, quantum phase estimation, and Hamiltonian simulation, which appear as subroutines for large families of composite quantum algorithms. A number of these quantum algorithms were recently tied together by a novel technique known as the quantum singular value transformation (QSVT), which enables one to perform a polynomial transformation of the singular values of a linear operator embedded in a unitary matrix. In the seminal GSLW’19 paper on QSVT [Gilyén, Su, Low, and Wiebe, ACM STOC 2019], many algorithms are encompassed, including amplitude amplification, methods for the quantum linear systems problem, and quantum simulation. Here, we provide a pedagogical tutorial through these developments, first illustrating how quantum signal processing may be generalized to the quantum eigenvalue transform, from which QSVT naturally emerges. Paralleling GSLW’19, we then employ QSVT to construct intuitive quantum algorithms for search, phase estimation, and Hamiltonian simulation, and also showcase algorithms for the eigenvalue threshold problem and matrix inversion. This overview illustrates how QSVT is a single framework comprising the three major quantum algorithms, thus suggesting a grand unification of quantum algorithms.
-
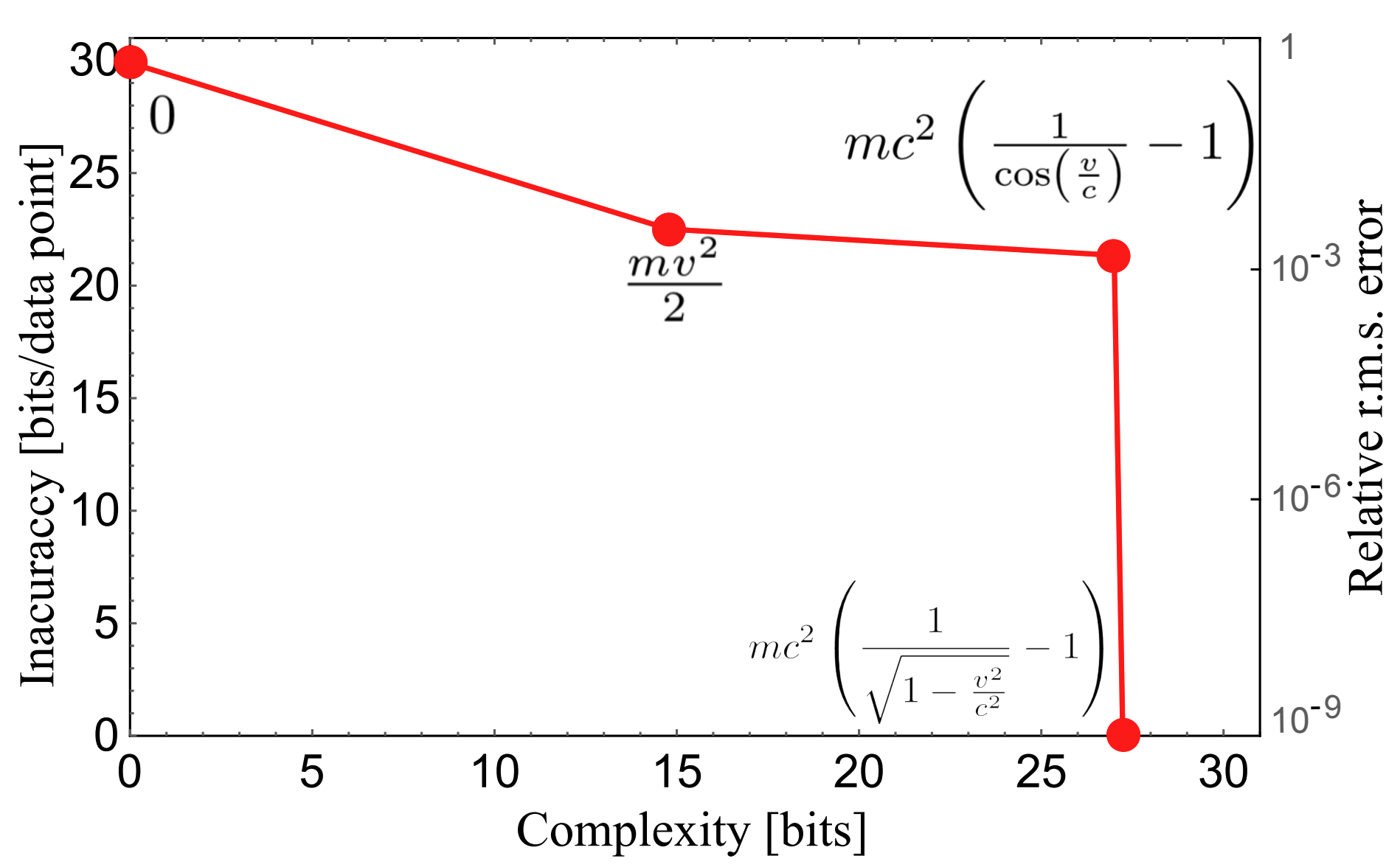 AI Feynman 2.0: Pareto-optimal symbolic regression exploiting graph modularityUdrescu, Silviu-Marian, Tan, Andrew K, Feng, Jiahai, Neto, Orisvaldo, Wu, Tailin, and Tegmark, MaxAdvances in Neural Information Processing Systems 2020
AI Feynman 2.0: Pareto-optimal symbolic regression exploiting graph modularityUdrescu, Silviu-Marian, Tan, Andrew K, Feng, Jiahai, Neto, Orisvaldo, Wu, Tailin, and Tegmark, MaxAdvances in Neural Information Processing Systems 2020We present an improved method for symbolic regression that seeks to fit data to formulas that are Pareto-optimal, in the sense of having the best accuracy for a given complexity. It improves on the previous state-of-the-art by typically being orders of magnitude more robust toward noise and bad data, and also by discovering many formulas that stumped previous methods. We develop a method for discovering generalized symmetries (arbitrary modularity in the computational graph of a formula) from gradient properties of a neural network fit. We use normalizing flows to generalize our symbolic regression method to probability distributions from which we only have samples, and employ statistical hypothesis testing to accelerate robust brute-force search.